Bayesian linear regression
Linear regression 이란..?
어떤 Dataset 내에서의 어떤 특성을 선형적으로 표현하는 과정
$$
y = b_0 + b_i * x_i^T
$$
위와 같은 선형방정식에서 x(입력 값)와 y(출력값) 사이간의 관계를 찾는 과정이다. 그래서 주어진 Dataset에서 x_1의 변화에 따른 y값의 변화량과, 이 변화값들이 b_0, b_1에 끼치는 영향을 찾아야한다. 이때 y는 x_1의 변화에 따라 변하는 값이기때문에 y를 Dependent Variable(DV) x_1을 Independent Variable(IV) 이라고 한다. 그리고 DV와 IV의 관계 비율을 결정하는 b_i을 Coefficent하고 하며 Linear Regression의 초기값을 결정하는 b_0, Constant라고 한다.
위의 상황에서 학습 데이터의 지점에서 최소 오차( |y_i - y_i^| )를 보이는 b_1, b_0를 구해 특정 line을 구할수 있다. 이때 양수 오차와 음수 오차의 계산을 통일하기 위해 오차 값의 제곱을 ( |y_i - y_i^|^2 )을 이용한다. 이와 같이 오차를 최소화하는 방법을 최소 자승법이라고 한다.
$$
y(x,w)=w_0+\sum_{j=1}^{M-1} w_j\phi_j(x)
$$$$
\phi_j(x)=exp{-\frac{(x-\mu_j)}{2s^2}} :basis function
$$
Bayesian regression
위에서 언급한 Regression(최소 자승법)이 오차를 최소화하는 방법이라면 베이지안 회귀는 가능도를 최대화하는 것에 목적이 있다. 베이지안 회귀의 가장 기본적인 선형모델은 다음과 같다.
$$
y = \theta_1x + \theta_2+ \epsilon
$$
θ_1, θ_2: 모델의 파라미터, y: DV, x: IV, ε: 오차
=> x,y의 관측값을 통해 θ_1, θ_2를 추정하는 것이다.
여기서 "가능도(likehood)"란 확률의 개념과는 조금 다르다.
확률(possiability) : 관측값이 나올 확률
가능도(likehood) : 독립적으로 추출 가능한 모든 관측값 x_i가 확률 밀도에서 갖는 값의 곱
평균이 μ, 표준편차가 σ인 선형 모델에서 확률 분포는 다음과 같은 식을 가진다.
$$
x ~ N(\mu,\sigma^2)
$$$$
f(x;\mu,\sigma) = \frac{1}{{\sigma\sqrt{2\pi}}}exp(-\frac{(x-\mu)^2}{2\sigma^2})
$$
위 식을에서 정의된 가능도를 추산하는 식을 정리하면 다음과 같다.
$$
likehood = L(\theta_1, \theta_2;x,y)= \Pi_{i-1}^N \frac{1}{{\sigma\sqrt{2\pi}}}exp(-\frac{(y_i-{(\theta_1x_i+\theta_2)})^2}{2\sigma^2})
$$
한편 베이즈 추론은 우리가 직접 알 수 없는 것들에 대해서 추론할때 모델을 상정하고 관측이 추론으로 이어지는 과정을 담는 추론 방법이다. 베이즈 추론을 알기 위해서는 베이즈 추론이 되는 베이즈 정리를 알아야 한다. 베이즈 정리에서는 사건 A, B가 있을떄 사건 A와 B의 교집합의 확률에 관점을 부여한다.
$$
P(A|B)=P(A|B)P(B)=P(B|A)P(A)
$$
베이즈 정리는 이 관점을 "B라는 조건에서 A가 발생할 확률"로 보는 조건부확률로 표현한다.
$$
P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{P(A|B)P(B)}{P(B)}
$$
이를 모델 관점에서 보면 관측할 수 있는 것을 B, 추론해야할 것을 A로 둔다. 즉 B는 데이터 A는 추론을 시행하는 모델이다.
모델A 입장에서 살펴보면 추정을 시행하는 모델 A의 확률 분포 P(A)에서 관측값 B가 가능한 확률, 즉 관측값 B가 모델 A에서 가능한 "가능도"를 곱해줌으로서 B가 가능한 조건에서 A가 가능한 확률 P(A|B)로 모델의 확률 분포가 갱신되는 것이다.
이 개념을 수학적으로 풀려고 하는 데 아주 복잡하다..
정리하자면 베이즈 추론이란 관측값을 통해, 모델의 확률분포를 업데이트 하는 추론이다. 베이지안 추론을 통해 선형회귀의 최대 가능도 방법을 시행하면서 발생할 수 있는 과적합 문제를 피할수 있으며 훈련 데이터를 통해 모델의 복잡도를 결정할수 있다는 장점이 있다.
하지만 문제가 있다. 관측값 B를 관측하기 전인 P(A)를 사전 분포, 관측값이 반영된 확률분포 P(A|B)를 사후분포라고 했을때 확률분포에 반영되어야할 관측값의 수가 늘어난다면 사후분포를 탐색해야하는 공간이 지수함수 꼴로 늘어나기 때문에 이에 대응하기 위한 전략을 마련해야 한다.
과적합 문제( Overfitting) : 훈련 데이터의 오차를 모두 반영되어 일반성을 상실한 상태
사후분포 탐색전략 - 마르코프 체인 몬테카를로법(MCMC)
마르코프 체인은 어떤 상태가 바로 이전 상태의 결과에 영향을 받는 상황을 의미한다. 그리고 몬테카를로는 무작위 샘플링을 말하는 것이다. 즉, 이 둘을 합치면 어떤 상태가 무작위적이지만 이전 상황에 의존적으로 움직이는(전이되는) 상황 을 말한다.
그래서 MCMC는 특정 조건의 마르코프 체인이 정상 상태 분포(steady-state distribution)를 나타내며 ergodic하다는 점을 이용한다. 여기서 정상 상태 분포가 ergodic하게 만들 수 있는 특정 조건은 1. 전이 상태가 하나의 값으로 정착 되지 않을 조건 2. 전이가 주기성을 띄지 않을 조건을 말한다. 베이즈 추론에서 수많은 관측값으로부터 MCMC를 적용하기 위해서는 앞서 말한 조건을 만족하는 형태로 샘플링을 진행해야 할것이다.
그래서 제시된 MCMC 샘플링 방식은 임의의 랜덤한 관측값에서 시작하되 이전값이 다음값에 영향을 주도록 i번째 표본을 참고해, 다음 i+1번째 표본을 선발하는 방식을 사용한다. 놀랍게도 관측값이 많으면 많을수록 실제 뽑아낸 확률분포와 비슷하게 수렴하게 된다고 한다.

다만 여기서 "임의의 랜덤한 관측값에서 시작하되 이전값이 다음값에 영향을 주도록 i번째 표본을 참고해, 다음 i+1번째 표본을 선발하는 방식"의 실제적 방법론은 다양한 MCMC 구현 알고리즘이 존재한다.
구현 MCMC 알고리즘 : Metropolis-Hastings 알고리즘
마르코프 체인 : 어떤 인과적 상황에서 여러상태{x_1,x_2, ....}들이 존재할 수 있음을 가정할때, 특정상황 x_i에서 이외 다른 상황 x_j로 상태가 전이될 조건부확률의 확률 분포는 정해져있는, 그래서 폐쇄된 Steady-state diagram을 그릴 수 있는 정상 상태 분포를 나타낼 수 있는 상황을 말한다. 위에서는 임의의 관측값에서 시작해 의도적으로 특정 파라미터를 기준으로 다음 관측 표본을 선정하는 상황 자체를 마프코프 체인이라고 보는 것이다.
Ergodic : 전체 표본에 대한 통계적 평균과 시간적 평균, 혹은 랜덤한 부분 집합의 평균이 동일한 특성을 보이는 성질. 다시말해 부분 집합에 해당하는 표본의 특성이 전체 표본의 통계적 특성을 대표할 수 있음을 표현하는 성질이다.
그래서 마프로프 체인에서는 위에서 언급한 2가지 조건이 만족하도록 MCMC가 구현된다면 전체 모집단의 통계(여기서는 확률분포)를 반영한다는 것이 수학적으로 증명되어 이용하는 것이다.
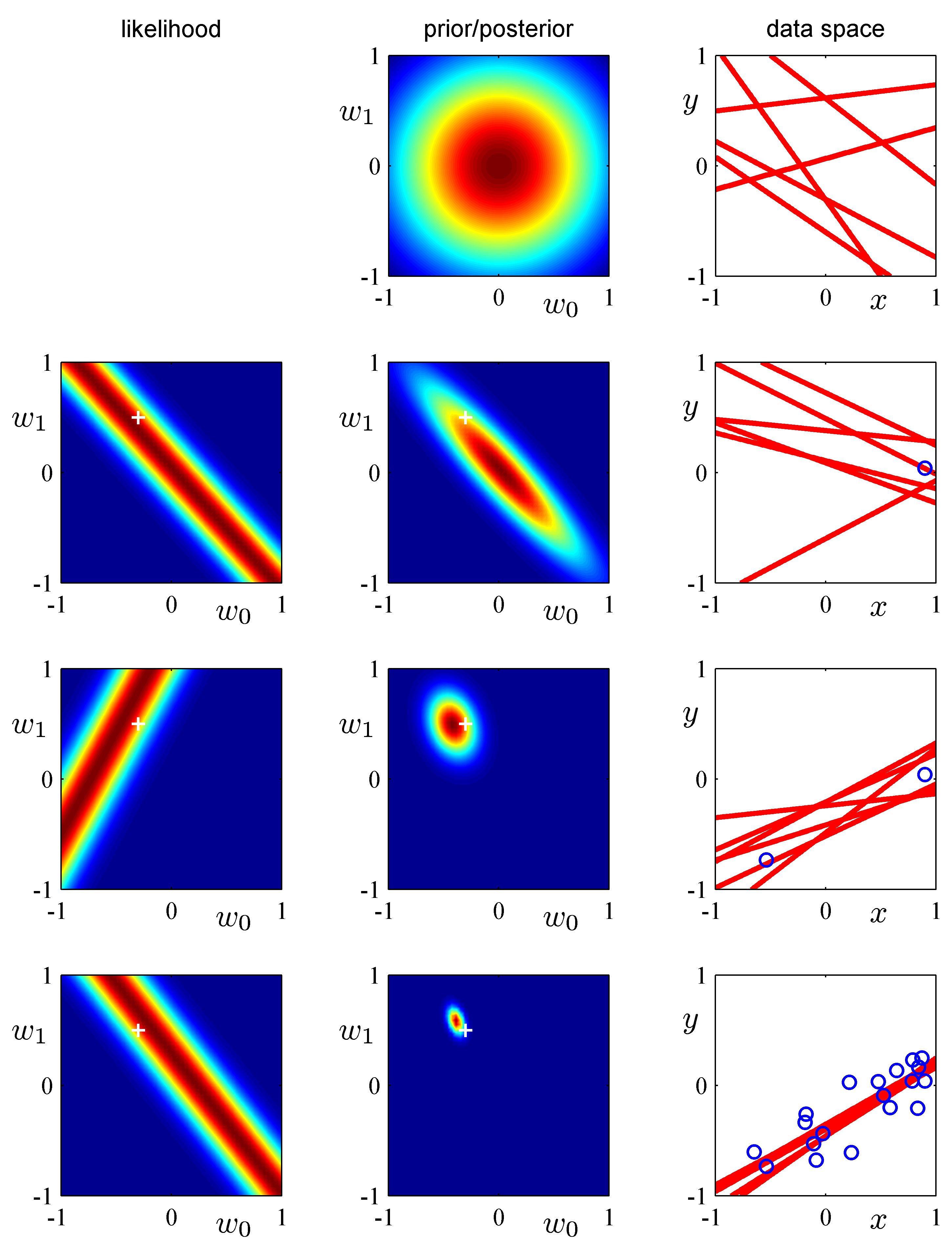
정리하자면 Bayesian regression 은 베이즈 정리를 기반으로 사전 확률 분포에서 MCMC기법에 의거, 선정된 관측값을 반영하여 사후 확률분포를 추산하는 방식으로 모든 관측값이 반영되었을 때 새로운 값 관측값(unobserved data) x에 대한 출력값 y를 확률 분포에 의거 결정할 수 있는 예측 분포 (Prodictive distribution) 를 만드는 모델이라고 할 수 있다.
Bayesian regression에서의 예측 분포(Predictive distribution)
unobserved data(y')에 대한 사전 예측 분포와 사후 예측분포는 다음과 같다. 여기서 사전예측분포는 사전 가능도 함수의 곱을 적분한 형태로 정의 된다. 이는 θ에 대한 가능도 함수의 평균이다. 사후예측분포는 새로운 관측결과 y와 확률 변수 y~의 관계가 독립이라 가정한다. 그래서 Unobserved data에 대한 가능도는 가능도와 Observed data의 곱으로 정의 된다. 왜라고 묻는다면 그 뒤에는 어려운 수학 수식들이 기다리고 있다.
- 사전 예측 분포
$$
p(\widetilde{y})=\int p(\widetilde{y},\theta)d\theta=\int p(\widetilde{y}|\theta)\times p(\theta) d\theta
$$
- 사후 예측 분포
$$
p(\widetilde{y}|y)=\int p(\widetilde{y},\theta|y)d\theta=\int p(\widetilde{y}|\theta,y)\times p(\theta|y) d\theta
$$
Bayesian logistic regression
logistic regression이란..?
회귀를 사용하여 요구되는 범주에 속할 확률을 0~1 사이의 값으로 예측하고 이 확률에 따라 더 가능성이 높은 범주에 속하는 편으로 분류해주는 지도학습 알고리즘이다. 선형회귀와 비교하자면 선형회귀는 +와 - 방향으로 무한히 뻗어 가나는데 이 경우 극단적인 표본에 있어서는 비현실적인 값(음수 확률)을 출력하게 된다.
로지스틱 회귀에서는 확률이 0과 1 사이의 값이 출력되는데 이 경우 아래 사진과 같은 극단에서 수렴하는 그래프를 그리게 된다.
로지스틱 회귀의 확률 예측 단계
모든 속성(feature)들의 계수(coefficient)와 절편(intercept)을 0으로 초기화한다.
각 속성들의 값(value)에 계수(coefficient)를 곱해서 log-odds를 구한다.
log-odds를 sigmoid 함수에 넣어서 [0,1] 범위의 확률을 구한다.
Log-Odds
선형회귀에서는 속성값(x)에 계수(coefficient)에 곱하고 절편(intercept)을 더해서 예측값을 구하는 방식이다. 로지스틱 회귀에서는 이와 예측값 대신에 log-odds를 구해야한다는 점에서 차이가 있다.
$$
Log-odds=log(\frac{P(event,occuring)}{P(event,not,occurring)})
$$
로지스틱 회귀에서는 선형회귀에서 처럼 예측값을 구하려면 dot product (내적)방식으로 log-odds를 구할수 있다.
각 속성들의 값이 포함된 행렬과 각 계수가 포함된 행렬은 다음과 같이 계산한다.
$$
z=b_0+b_1x_1+\cdots+b_nx_n
$$$$
\begin{bmatrix}
b_0\
b_1\
b_2\
\vdots
\end{bmatrix}
\begin{bmatrix}
x_0
x_1
x_2
\cdots
\end{bmatrix} =
b_0 x_0+b_1 x_1+b_2 x_2
$$
Sigmoid Function
로지스틱 회귀에서 확률을 0과 1사이의 커브 모양으로 나타나게 해주는 것이 Sigmod 함수이다.
위에서 도출된 Log-odds를 sigmoid함수에 대이하여 0과 1사이의 값으로 변환해주는 것이다.
확인 결과 Bayesian logistic regression은 분류 모델에 해당해 본 과제에는 우선 관련사항이 없는것으로 판단된다.
Catboost
Boosting algorithm이란?
머신러닝 앙상블 기법중 하나로 약한 학습기 여러개를 순차적으로 여러개 결합하여 예측과 분류의 성능을 높이는 알고리즘
여러개의 알고리즘이 순차적으로 학습 예측 하면서 이전에 학습한 알고리즘의 예측이 틀린 데이터를 올바르게 예측할수 있도록 다음알고리즘에 가중치를 부여하여 학습과 예측을 진행하는 방식
앙상블 : 여러 단순한 모델을 결합하여 정확한 모델을 만드는 방법
의사 결정 트리(Decision Tree)
일련의 분류 규칙을 통해 데이터를 분류, 회귀하는 지도학습모델, 결과 모델이 Tree 구조이다. 특정 기준에 따라 데이터를 구분하게 되며 한번의 분기 마다 변수영역을 두개로 구분한다. 여기서 나온 질문이나 정답을 노드(Node)라고 한다.
의사 결정 트리의 기본 아이디어는 말단노드가 가장 섞이지 않은 상태에서 분류되는 복잡성(Entropy)가 가장 낮도록 만드는 것이 핵심이다.
불순도(impurity)
의사 결정 트리에서 분기 기준을 선택하기 위해서는 불순도라는 개념을 사용한다. 이는 복잡성을 의미하며 범주 안에 서로 다른 데이터가 얼마나 섞여있는지를 의미한다. 다양한 범주의 개채가 섞여 있을수록 불순도가 높아진다.
분기 기준을 정할때 현재 노드보다 자식 노드의 불순도가 더 낮도록 설정해야한다.
그래서 자식노드가 부모 노드에 비해 불순도가 낮아진 정도를 정보 획득(Information Gain) 이라고 한다.
불순도를 정량적으로 평가 할수 있는 함수는 대표적으로 2가지 종류가 있다.
지니 지수(Gini)
$$
I(A) = 1-\Sigma_{k=1}^m p_k^2 ; [range: 0 \sim 0.5]
$$
엔트로피 지수(Entropy)
$$
E = -\Sigma_{i=1}^{k} p_i\log_2(p_i) ; [range: 0 \sim 1]
$$정보 획득
만일 불순도가 1인 상태에서 0.7로 바뀌게 되면 정보획득은 0.3이다
의사 결정 트리의 구성단계
Root노드의 불순도 계산
나머지 속성에 대해 자식노드의 불순도 계산
각 속성에 대한 정보획득 값이 최대가 되는 분기 조건을 찾아 분기
모든 leaf 노드의 불순도가 0이 될때까지 2~3 과정 수행
모든 말단 노드의 불순도가 0이 되면 이러한 상황을 Full tree(최대 트리)를 형성하게 됨. 그런데 이런 최대트리 상황은 데이터의 과적합 문제(Overfitting)를 일으켜 일반화의 성능이 떨어지게 된다.
따라서 형성된 결정트리에 대해 가지치기(Pruning)을 수행해 일반화 성능을 올림
의사결정 트리의 가지치기 비용함수
- 비용함수는 가설이 얼마나 정확한지 판단하는 기준을 책정해주는 함수로 의사결정트리에서 일반화를 위한 가지치기를 통해 최대한 비용이 가장 작은 가지치기를 찾는것을 목적으로 한다. 그 정의는 다음과 같다.
$$
CC(T) = Err(T) + α × L(T)
$$CC(T) = 의사 결정 트리의 비용복잡도
ERR(T) = 검증 데이터에 대한 오분류율
Alpha = ERR과 L의 결합 가중치
L(T) = terminal node의 수(트리구조의 복잡도)
데이터 전처리와 수치형 변수 범주형 범주를 한꺼번에 다룰수 있다는 장점이 있다.
과적합으로 인해 알고리즘의 성능이 떨어징수도 있도 한번에 하나의 변수만 고려하기 때문에 변수의 상호작용을 파악하기 어렵다. 그리고 데이터의 변동에 민감하다.
이러한 의사 결정트리의 문제점을 보안한것이 "Random forest"이다.
랜덤 포레스트(Random forest)
의사 결정트리는 과적합 문제가 발생할 가능성이 크다. 그래서 의사 결정 트리에서는 Puruning을 통해 트리의 최대 높이를 제한해 과적합 문제를 피하려고 하지만 한계가 있다. 랜덤 포레스트는 좀더 일반화된 트리를 만드는 것에 목적이 있다.
Bagging: 트리를 만들때 trainging Set의 부분집합을 활용하여 형성하는 것. 모든 트리는 서로 다른 데이터를 바탕으로 형성하지만 training set의 부분집합이다. 부분집합을 형성할때에는 중복을 허용한다.
Bagging Feature: 데이터의 Feature 또한 부분 집합으로 활용한다. 일반적으로 M^{1/2}의 개수만큼 선택하며 트리가 만들어 질때까지 해당과정을 반복한다. 그래서 만들어진 트리중 information gain이 가장 높은 feature을 선택하여 데이터를 분류한다.
classify: Bagging에서 형성된 여러개의 트리를 통해 임의의 데이터의 분류 결과 값 경향성을 확인하고 최종적으로 결과를 분류함.
AdaBoost(Adaptive Boost)
관측치들에 가중치를 더하면서 동작하는 모델. 분류하기 어려운 데이터에는 가중치를 더하고 잘 분류되어진 데이터에는 가중치를 덜하는 방식으로 부스팅을 수행한다. 약한 학습기(weak Learner)로서 의사 결정 트리(Decision Tree)를 사용한다. AdaBoost에서는 노드 2개짜리 tree model(stump)을 이용해 부스팅을 진행한다.
전체 데이터 random sampling
모든 sample 데이터 가중치 초기화
weak learner를 만들고 학습의 error를 계산해 데이터의 가중치와 모델 가중치를 확인한다.
error를 바탕으로한 데이터 가중치로 업데이트한다.
데이터 가중치를 기반으로 모델 가중치를 계산한다.
3~5 번 과정을 충분히 반복한다.
모델 가중치를 Normalize 하고 최종모델을 도출한다.
$$
W_i=1/n, i=1,\ldots,n
$$$$
err_m=\Sigma_{i=1}^{n}W_i
$$$$
c_m=\frac{1}{2}\log((1-err_m)/err_m)
$$$$
w_i =w_i\cdot exp(-c_m\cdot y_i \cdot \hat f_m(x_i))
$$
Gradient Boosting(GBM)
Residual fitting은 아주 간단한 모델 A를 통해 y를 예특하고 생긴 잔차(Residual)을 다시 B모델을 통해 예측하는것이다. 이를 통해 A+B모델을 통해 y을 예측하면 A보다 나은 B모델을 만들수 있고 점차 잔차가 줄어들며 trainig set을 잘 설명해주는 예측 모델을 만들수 있게 된다.
해당 모델을 통해 bias를 줄일수 있으나 과적합의 위험이 있기 때문에 smapling, penaliaing, regularization 같은 테크닉을 이용해 사용하는 것이 보편적이다.
penaliaing: 목적성을 띄기 위해서 가중치를 주는 기술을 뜻한다.
regularization: 일종의 패널티 조건으로서 복잡한 쪽 보다 단순한 쪽을 선택하게 함으로서 일반적으로 더 좋은 학습결과를 하게 만드는 테크닉이다.
Residual fitting과 Gradient의 관계는 Residual(잔차)를 만약 loss funtion를 sqaured error라고 한다면 이를 순차적으로 다음 모델로 넘겼을때 다음 residual이 negative gradient가 된다고 한다.
$$
j(y_i,f(x_i))=\frac{1}{2}(y_i-f(x_i))^2
$$$$
\frac{\partial j(y_i,f(x_i))}{\partial f(x_i)}=\frac{\partial[\frac{1}{2}(y_i-f(x_i))^2]}{\partial f(x_i)}=f(x_i)-y_i=-(y_i-f(x_i))
$$이렇듯 GB에서는 다음모델을 만들때 negative gradient를 이용해 만들기 때문에 gradient boosting이라고 한다.
negative gradient는 직관적으로 어떤 데이터 포인트에서 loss fuction이 줄어들기 위해 f(x)로 가려는 방향이가. 이 방향에서 새로운 모델을 fitting해서 이전 모델과 결합하면 f(x)는 loss fuction이 줄어드는 방향으로 업데이트 되는 것이다. 그래서 어러한 아이디어를 Gradient Boosting이라고 부르는 것이다.
최초값을 weight의 평균값으로 예측
예측값과 실제값 사이의 오차 구하기
계산된 오차를 다른 데이터셋 Feature를 가지고 Tree를 만들기
분류된 값들은 평균을 매김(트리완성)
완성된 트리에 새 데이터를 넣고 나온 wieght값이랑 이전에 평균 weight값이랑 더한다. 이때 과적합을 피하기 위해 learning rate를 곱해준 만큼 더해서 새로운 residaul을 만들어준다.
남은 데이터들도 5번과정을 수행하고 나온 residual 로 업데이트 해준다.
2~5본 과정을 반복하면서 점점 오차다 줄어들고 Hight Variance를 피하면서 천천히 학습을 해나간다.
GB 또한 완전히 과적합 문제에서 자유롭지 못하며 수행시간이 느리다는 단점이 있다.
XGBoost(XGB)
GB가 병렬 학습이 지원되도록 구현한 알고리즘으로 회귀 문제와 분류 문제를 모두 지원하고 효율이 좋다.
구현 라이브러리 설명 : https://wooono.tistory.com/97
Light GBM
파라미터 튜닝이 번거로운 XGB를 보안하기 위해 만들어진 알고리즘으로 성능을 유지한 채 학습시간을 상당히 단축시킨 모델이다.
기존의 GB는 균형트리방식(Level wise)을 사용해 학습을 진행했다. 이는 균형잡힌 트리를 생성하면서 깊이를 최소화 할수 있다는 장점이 있고 과적합에 더 강하지만 균형을 맞추는 과정에서 더 시간이 걸린다는 문제가 있다
그래서 LightGBM은 리프 중심 트리 분할(Leaf wise) 방식을 사용해 트리의 균형을 맞추지 않고 최대 손실값(max leaf loss)를 가지는 리프 노드를 계속 분할래서 깊고 비대칭적인 트리를 만든다. 이와 같은 방식을 통해 균형 트리 방식보다 예측 손실 오류를 최소화 할수 있다.
구현 라이르러리 설명 : https://kimdingko-world.tistory.com/184
깊이가 깊은 트리를 형성하기에 하이퍼 파라미터 설정시 최대 깊이 설정이 중요하다.
약간 그리디 알고리즘 느낌이다..
CatBoost
CatBoost의 경우 GB와 같은 균형트리방식(Level wise)을 사용해 학습을 진행한다.
Order Boosting: 데이터 셋의 일부를 뽑아 잔차를 계산하고 모델을 만든다. 그리고 해당 모델로 나머지 데이터의 잔차를 예측하고 예측한 값을 가용해 업데이트 한다.
Random Permutaion: 데이터를 셔플링한 후 데이터를 뽑아내고 트리를 다각적으로 볼수 있도록한다.
Orderd Target Encoding: 범주형 변수를 인코딩 할때 임의의 선정된 데이터 외에 선정되지 못한 데이터의 타겟값까지도 엔코딩 되는 현상인 Data leakage를 피하기 한다.그래서 이전 데이터들의 타겟값을 기억해 두었다가 이전에 사용된 데이터의 타겟값만 업데이트 하는 기법이다.
Encoding 관련 자료 : https://dailyheumsi.tistory.com/120
Categorical Feauture Combinations : 서로 다른 두개의 카테고리가 명확하게 서로다른 성질을 보이는 경우 두개의 카테고리를 하나로 합쳐 생각한다.
One-hot Encoding : Target Encoding이 비효율 적인 범주형 변수를 처리할 때는 One-hot Encoding을 수행하는 기법
One-hot Encoding: 범주형 변수의 출현빈도로 변환하는 엔코딩 방식을 말한다. (범주 -> 수)
Optimized Parameter tuning : XDB, light GBM의 경우 파라미터 설정이 까다로우나 CatBoost는 내부 알고리즘을 이용해 이러한 까다로운 파라미터 설정을 안해도 결과에 영향을 주지 않는다.
대신 희소 행렬은 처리 하지 못하며 데이터가 대부분 수치형 변수 일경우 CatBoost보다 light GBM이 유리하다고 한다.
Reference
Bayesian Neural Network (베이지안 뉴럴 네트워크) 내용 정리 - gaussian37
https://mons1220.tistory.com/211
http://www.ktword.co.kr/test/view/view.php?m_temp1=4188
Variational Inference, 베이지안 딥러닝 | JuHyung Son
https://dailyheumsi.tistory.com/136
5. Bayesian Logistic Regression
https://hleecaster.com/ml-logistic-regression-concept/
https://ko.wikipedia.org/wiki/%EB%A1%9C%EC%A7%80%EC%8A%A4%ED%8B%B1_%ED%9A%8C%EA%B7%80
https://hyunlee103.tistory.com/25
https://dailyheumsi.tistory.com/136?category=877153
https://wooono.tistory.com/104
https://kimdingko-world.tistory.com/184
https://gentlej90.tistory.com/100
'공부 학습' 카테고리의 다른 글
| C++에서 virtual(가상함수) 란..? (0) | 2022.08.01 |
|---|---|
| 게임 서버의 이해 (0) | 2022.07.27 |
| Catboost 기본부터 알아보기 (0) | 2022.04.02 |
| 베이지안 선형 회귀(Bayesian linear regression) 기본부터 알아보기 (1) | 2022.04.02 |
| 네트워크 CH4 - Network Layer 3 (0) | 2021.05.04 |

